天道有轮回,苍天绕过谁~!(曾经偷过的懒,终究都要偿还的!)
这次来偿还 时间复杂度 的债了
时间复杂度
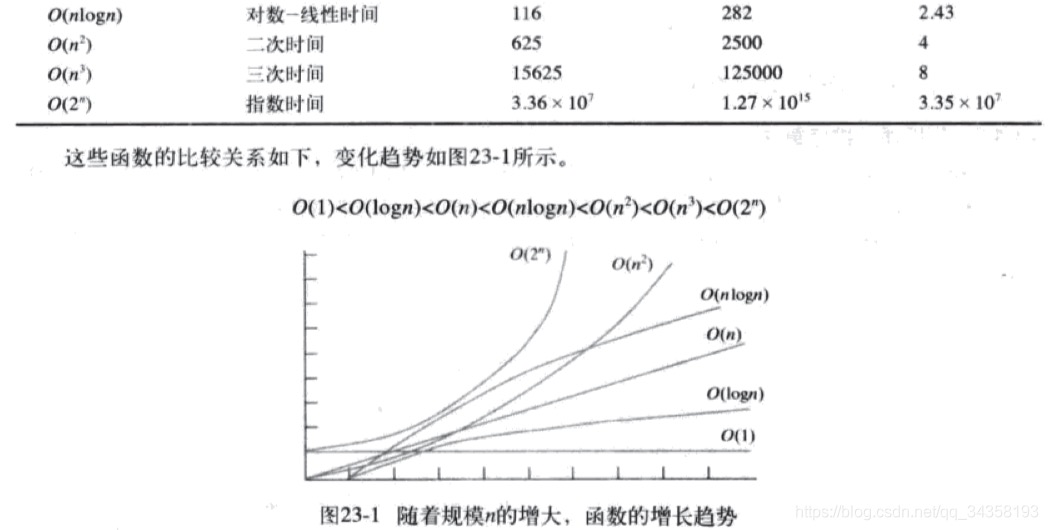
O(1)<O(log(n))<O(n)<O(n×log(n))<O(n2)<O(2n)
| 类型 |
意义 |
举例 |
| O(1) |
最低复杂度,常量值,也是耗时,耗空间与输入数据大小无关,无论输入数据增大多少倍,耗时/耗空间都不变 |
哈希算法就是典型的O(1)时间复杂度,无论数据规模多大,都可以在一次计算后找到目标(不考虑冲突的话) |
| O(n) |
数据量增大几倍,耗时也增大几倍 |
遍历算法 |
| O(log(n)) |
当数据增大倍时,耗时增大log(n)倍(这里的log是以2为底的,比如说,当数据增大256倍时,耗时只增大8倍) |
二分查找就是O(log(n))的算法,每找一次排除一半的可能,256个数据中查找只要找8次就可以找到目标 |
| O(n2) |
对n个数排序,需要扫描n×n次 |
冒泡排序 |
| O(n×log(n)) |
就是n乘以log(n),当数据增大256倍时,耗时增大256*8=2048倍。这个复杂度高于O(n)低于O(n2)。 |
归并排序就是O(n×log(n))的时间复杂度。 |
常见排序的时间复杂度
稳定性表示,排序后两个相等的键值的顺序和排序之前的顺序相同
| 排序算法 |
平均复杂度 |
最好情况 |
最坏情况 |
空间复杂度 |
排序方式 |
稳定性 |
| 冒泡排序 |
O(n2) |
O(n) |
O(n2) |
O(1) |
In-place |
稳定 |
| 选择排序 |
O(n2) |
O(n2) |
O(n2) |
O(1) |
In-place |
不稳定 |
| 插入排序 |
O(n2) |
O(n) |
O(n2) |
O(1) |
In-place |
稳定 |
| 希尔排序 |
O(n×log(n)) |
O(n×log(n)) |
O(n×log(n)) |
O(1) |
In-place |
不稳定 |
| 归并排序 |
O(n×log(n)) |
O(n×log(n)) |
O(n×log(n)) |
O(n) |
Out-place |
稳定 |
| 快速排序 |
O(n×log(n)) |
O(n×log(n)) |
O(n2) |
O(log(n)) |
In-place |
不稳定 |
| 堆排序 |
O(n×log(n)) |
O(n×log(n)) |
O(n×log(n)) |
O(1) |
In-place |
不稳定 |
| 计数排序 |
O(n+k) |
O(n+k) |
O(n+k) |
O(k) |
Out-place |
稳定 |
| 桶排序 |
O(n+k) |
O(n+k) |
O(n2) |
O(n+k) |
Out-place |
稳定 |
| 基数排序 |
O(n×k) |
O(n×k) |
O(n×k) |
O(n+k) |
Out-place |
稳定 |
